Capacity Planning Algorithms Supported by Sprinklr WFM
Updated
Accurate Capacity Planning is vital for Sprinklr to optimize resources within Workforce Management (WFM). It ensures efficient alignment of human and technological resources with dynamic customer demands thereby improving operational effectiveness and sustaining higher service standards. Some of the Capacity Planning algorithms that Sprinklr employs are detailed as:
Note: Capacity Planning will be deprecating upcoming releases, and its functionality will be integrated into Forecast Scenarios.
Erlang C
The Erlang C model calculates the number of agents (also called Full-Time Equivalents (FTEs)) required based on inbound traffic and service level objectives in contact centers. It considers the probability that a customer will have to wait for service and is particularly useful for scenarios with a large number of inbound volumes. Erlang C uses parameters such as Average Handling Time, SLA, Service Time Threshold.
Intended Usage
For calculating resource attributes like incoming calls offered, emails offered, and text messages offered for a
vertical.Finding the optimal number of agents.
Calls and other digital modes (Email, WhatsApp messages) detection at a particular time interval using trained model.
The Erlang C model uses the following parameters:
Average Handling Time: The average duration taken to handle a customer call, from initiation to closure.
Service Level Adherence: A quantitative metric used in call centers to evaluate whether agents are adhering meticulously to their scheduled work hours and maintaining the pre-established service quality standards. In Sprinklr, it is the percentage of calls answered within a specified duration.
Average Speed of Answer: The average time it takes for a customer's call to be answered by an agent.
Shrinkage: The percentage of time agents are unavailable to handle customer calls due to breaks, training, meetings, and so on.
Occupancy: The percentage of time that call center agents spend on active communication with customers, excluding idle time.
Service Level Calculation
![]()
In this equation, the term [P_w×e^(-[(N-A)×((Target Time)/AHT)])] provides the average wait time of a customer.
The term e^(-[(N-A)×((Target Time)/AHT)]) describes the expected average queue waiting time of customers (not the exact time), under an exponential distribution of waiting times assumption. It is exponential because the assumption is mostly based on queuing theory, which means in practical situations, including queuing systems like call centers, the distribution of waiting times can often be well-approximated by what is called an exponential distribution. As exponential distribution possesses the memoryless property, the time until the next event (for example, the next customer arriving) does not depend on how much time has passed since the last event.
Sample Calculation of Service Level
Assume the following values:
Wait Probability (P_w): 0.3
Number of agents (N): 50
Number of agents actually available (A): 45
Target Time: 20 seconds
Average Handling Time (AHT): 300 seconds
Plugging these values into the above mathematical expression gives a Service Level of approximately 0.7849, or 78.49%. This means that about 78.49% of the calls are expected to be answered within the target time of 20 seconds.
Wait Probability Calculation
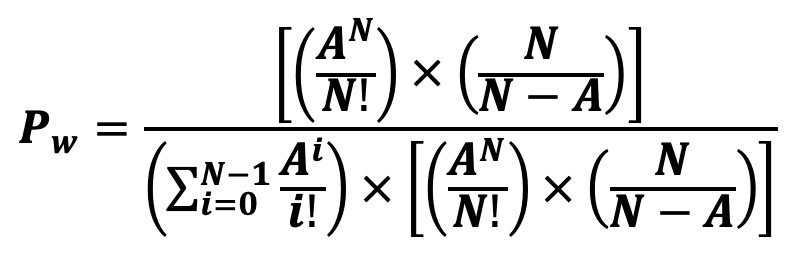
This equation can be understood like any probabilistic equation:
The numerator denotes the probability of all servers being busy (and thus, someone must wait) adjusted by the remaining capacity.
The denominator denotes the total probability, which includes all possible states (from 0 customers up to N-1 customers) plus the state where all servers are busy.
Understanding the Wait Probability (P_w) Formula
In this section, we will understand the components of the mathematical expression for Wait Probability.
Explaining the Terms in the Numerator
(A^N/N!): The probability that all servers are busy in a system with Poisson arrivals and exponential service times. The formula explains that, under the intensity A, the chance that we have exactly N customers being served simultaneously. Hence, it captures the combinatorial ways the system's load A distributes among exactly N workers.
(N/(N-A)): This term reflects the impact of having customers arrive at a rate A into a system with N servers. As A approaches N, the system's servers become highly utilized, increasing the likelihood that any arriving customer will have to wait.
Thus, these two terms together denote the probability of all servers being busy (and thus, someone must wait) adjusted by the remaining capacity, when multiplied together.
Explaining the Terms in the Denominator
The term (N/(N-A)) is present in both the numerator and the denominator, which denotes the probability of all workers being busy.
The term (
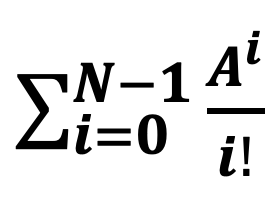 ) is the combined probabilities of all states where fewer than N workers are busy. This term ensures that every possible scenario of partial server utilization is included in determining the overall system's behavior.
) is the combined probabilities of all states where fewer than N workers are busy. This term ensures that every possible scenario of partial server utilization is included in determining the overall system's behavior.
Sample Calculation of Wait Probability
Assume the following values:
Traffic intensity (A): 10
Number of agents (N): 5
Plugging these values in the above mathematical expression for Wait Probability gives a Wait Probability of approximately 0.00155 or 0.155%. This means there is a probability of 0.155% that a call will have to wait before being answered.
Occupancy Calculation

The percentage of time call center agents spend on customer interactions. The aim is to keep the agent's maximum occupancy below the specified threshold.
The number of agents is not increased to adjust the occupancy involved.
By calculating Service Level and Occupancy, you can get the agents that suffice the service level for the given number of transactions (or call volume).
The equation is tuned to give precise values in float places by updating the internal mathematics to improve the waiting time calculations of a Queue.
Sample Calculation of Occupancy
Assume the following values:
Traffic Intensity: 30 Erlangs
Number of Raw Agents: 40
Plugging these values in the above mathematical expression for calculating Occupancy gives a 75%. This means that each agent is occupied with calls 75% of the time.
ErlangCCustom
For Fractional Support, we have added support for ErlangCCustom, which does the following things differently:
Calculation of agents on a fractional level: The calculation of clients is done on a more granular level, unlike the standard “ErlangC” class, which yields only an integral number of agents.
Improvement on calculation of Service Level: Sometimes "ErlangC" tends to predict very small Service Level, when the original Service Level on the same set parameter by intuition is much higher.
Improvement on Occupancy: The calculation of "ErlangC" assumes every request was catered to and makes this calculation in occupancy, which we improved with the number of requests that were fulfilled.
Scenario
A contact center receives 600 calls per hour. The Average Handling Time (AHT) is 5 minutes per call. The business goal is to achieve a Service Level Agreement (SLA) of answering 80% of calls within 20 seconds while maintaining an agent occupancy of 85%.
Step-by-Step Application
Calculate Traffic Intensity (Erlangs), which is a measure of the workload being placed on a service system, such as a call center.
Traffic Intensity = Calls Per Hour * AHT (in hours) = 600 * 5/60 = 50
Estimate Initial Number of Agents Required: Using the Erlang C formula and assumptions:
SLA: 80% of calls answered within 20 seconds.
Occupancy target: 85%.
Verify SLA Compliance: Apply the Erlang C formula to check whether the initialized agents can maintain the service level:
Wait Probability: Calculate the likelihood that incoming calls will wait in the queue.
Average Speed of Answer (ASA): Use Wait Probability to determine how quickly customers are served.
If the current number of agents cannot achieve the SLA, then they should increase the number of agents.
Validate Occupancy: Check if agent occupancy of agents remains below the 85% target, calculated as:
Occupancy = Erlangs/Raw Agent * 100.

Adjust for Shrinkage: Incorporate shrinkage (for example, breaks, training, absenteeism). Assuming a 30% shrinkage rate:
Required Agents = (Calculated Agents (or Raw Agents)/(1 - Shrinkage)) = 58.82/(1-0.3) = 84.02.
A simulation would require 84.02 agents (the exact number is slightly larger, 84.03361344537817, as rounded off for simplicity of calculation), according to ErlangCCustom implemented by Sprinklr.
Conclusion
To handle 600 calls per hour with a 5-minute AHT, an SLA of 80/20, and 30% shrinkage, the contact center requires 84.033 agents. This ensures that service levels and agent occupancy targets are met.
Unitary Method
The Unitary Method is a mathematical approach used to estimate the number of contact center agents required. It assumes linear scaling, which is a constant relationship between the inbound traffic and the amount of work performed by each contact center agent. In the Unitary Method, we assume that a call lasts M minutes, and we receive C calls in an interval of I minutes. In this scenario, the minimum number of agents that will be required for this interval will be ((C * M)/I), where the numerator is the total incoming traffic time, and the denominator is the interval size. This method gives us the minimum number of agents required to handle the incoming traffic for an interval.
Use Case
The Unitary method is employed in WFM Capacity Planning for quick and initial estimations, especially when a basic linear relationship between inbound volume and the task is sufficient. This method provides a rapid assessment of staffing needs.